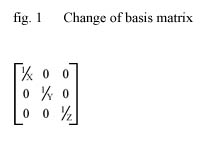pxdtut10.zip
How to read this document :
First of all let me say : This stuff is NOT easy!! It'll take a long time to understand
correctly and probably several readings of this text. So give yourself time to fully
understand what's written in a section before moving on to the next.
To fully understand the theory presented you will need to have a fairly good idea about
linear algebra - i.e. vectors, matrices, vector spaces and the like.
The tutorial is split up in two major parts - one on collision detection and one on
collision response. Now what's the difference I hear you ask ?
Collision detection deals with finding out whether or not we'll bump into something
when we move our ellipsoid though 3d space and if so, what do we hit and where ?
Collision response deals with what to do when a collision DO occur. Do we stop? Do we
continue movement in another direction ? What do we do ?
Collision response is important for the FEEL of the game you produce.
We will assume that the mesh is placed in the same space as the player - in world space. In
other words we assume that each mesh's world matrix is the identity matrix. I'll discuss
moving or displaced geometry in the section called "Dynamic geometry".
Vector spaces & translations between them :
This algorithm makes heavy use of non-standard vector spaces to simplify certain calculations.
Those of you already familiar with the definition of vector spaces and change-of-basis matrices
to move between spaces can skip this section entirely. The rest of you read on but be aware
that this is only a very quick crash-course on this matter. A full explanation would include
too much math and is beyond the scope of this tutorial anyway.
OK, most of you will never have encountered any other vector spaces than the standard two and
three dimensional spaces we usually think of from school math. These are called R2 and
R3 and are those we use in a standard coordinate system (like the one d3d or openGL operates in).
As it turns out we can easily define vector spaces or 4,5 or even infinitely (!!) many dimensions
by listing a few rules (axioms) which every vector space must follow. R2 and R3
follows these rules too!
Of course humans cannot visualize spaces of dimension greater than 3 and this might be the
greatest challenge when trying to work with such spaces. Still such spaces can be useful to a
game programmer. To give an example I can mention the quaternion which can be thought of as
vectors in 4D.
They are sometimes used to represent orientations for animations because we can interpolate smoothly
between them by using the shortest arc on a 4D unit sphere (this is called SLERP). The 3D alternative
is to store orientations in matrices and we all know you cannot interpolate between two matrices.
Don't worry though, we'll stay in 3D today - the above just goes as a motivation for the use of
"non-standard" vector spaces :)
OK, so here are the rules or axioms every vector space must follow :
It must be closed under addition and scalar multiplication. This means that given two vectors
from the vector space, say X and Y, then Z = X + Y
must also be in the same space. For any real number r (1, 3, 0.23423 etc.) if X
is in the space then so must r*X.
Informally said we cannot ever "leave" the vector space using these operations.
It must contain a zero-vector V0 so for all vectors X in the space
V0 + X = X. For all vectors X is must also be true that
X*0 = V0.
it must follow standard mathematical rules such as the associative law, commutative law etc.
Now I'll introduce to you the concept of a linear combination of vectors from a vector space.
Said in words it's what you get if you combine vectors from the space using addition and multiplication
with scalars (real numbers). For example if you have vectors X, Y and Z
you could combine them like this : V = 2*X + 4*Y + (-3)*Z
OK, what can we say about V? Well, from rule number 1 above we can see that V must belong
to the same vector space as X, Y and Z. Cool, that's what we need to really
define a basis for a given vector space.
A basis for a vector space is a collection of vectors belonging to the space for which the following
holds :
Every vector in the vector space is a linear combination of vectors from the basis.
Each of the vectors in the basis can NOT be made from a linear combination of the
other basis vectors.
The minimal number of vectors necessary to create a basis for a vector space is equal to the
vector space's dimension. So how many vectors are in R3s basis ?
I think it's time to take a break from the abstract definitions above and look at a familiar example.
After reading and understanding this example you should understand the stuff above good enough for
this tutorial. Lets look at the standard 3D vector space we know as R3. Is it a vector space ?
Well, we check the rules (very informally) :
Is it closed under addition ? If we have two vectors from R3, say x=(2,5,4) and
y=(6,3,8), is z=x+y in R3 ?
Well z = (2,5,4)+(6,3,8) = (8,8,12) - we believe this is in R3.
For any real number r, say r=2, is r*x in R3 ?
r*x = 2*(2,5,4) = (4,10,8). Check! First rule holds.
Is there a zero vector ? Yes, we use V0 = (0,0,0) and the rule holds. (You can check)
Third rule involves a lot of checks which are tedious so I'll just mention the commutative law
saying that x + y = y + x. Obviously that holds..
So R3 is a vector space! What is its basis ? The basis for R3 is called the 'standard basis' and
contains 3 vectors (e1,e2,e3). What are those vectors ? They are :
e1 = (1,0,0)
e2 = (0,1,0)
e3 = (0,0,1).
Well, if that is indeed the basis for R3 then we should be able to derive ANY vector from R3 as a linear
combination of those vectors right ? Well, we'll have to convince ourselves about this so given any vector from R3,
say v=(5,2,4), can we derive this from a linear combination of (e1,e2,e3)?
Yes, because 5*e1 + 2*e2 + 4*e3 = 5*(1,0,0) + 2*(0,1,0) + 4*(0,0,1) = (5,2,4) = v
It's clear that e1 cannot be made from e2 and e3 because no matter how you combine e2 and e3 the first
vector component would still be zero right? Same can be said for the other two basis vectors.
Now for an important definition! The coordinate for a point in a vector space is the
scalars multiplied to the basis vectors in the linear combination for the point!! In the example above
the point v has the coordinate (5,2,4).
This might seem obvious because we're used to working with R3 but make sure you see WHY
that is indeed its coordinate :
v = 5*e1 + 2*e2 + 4*e3 so the scalars are (5,2,4)
- get it ?
By now you should be convinced that R3 is a vector space following the axioms for general vector spaces.
It should also be clear that other vector spaces could exist - even other spaces of 3 dimensions.
For example what about the vector space made from the basis v1=(2,0,0) v2=(0,2,0) and
v3=(0,0,2). Which vectors does this space contain ? The same ones as R3 of course but with
different coordinates!!
Given a point (2,2,2) in R3 - which coordinate would that same point have in our new space ?
It would have the coordinate (1,1,1) because:
1*v1 + 1*v2 + 1*v3 = 1*(2,0,0) + 1*(0,2,0) + 1*(0,0,2) = (2,2,2).
This is exactly the trick we'll use in this tutorial to create a very special vector space which has the
property that the ellipsoid we're using to model our player with becomes a unit-sphere in that space!!
A unit sphere is a sphere with radius = 1 but it's also an ellipsoid with radius VECTOR = (1,1,1), right?
So how do we create such a space ? Well, we'll have to come up with a basis for the space. If the
ellipsoid is defined by a radius vector of (x,y,z) we'll just chose the basis to be :
v1 = (x,0,0)
v2 = (0,y,0)
v3 = (0,0,z)
Now in this space the ellipsoids radius vector will be (1,1,1), right? And you can
check if that choice really is a valid vector space if you want - or you can take my word for it (generally not
recommended ;)
The LAST thing we need to know is how to translate a point from R3 into our
new vector space. We're in luck, because it turns out that because linear combination is a linear function we can
get away with just describing what to do with the 3 basis vectors (e1,e2,e3) (remember these from above?).
We find that if we use the basis (v1,v2,v3) from above, then :
e1 = 1/x * v1 + 0 * v2 + 0 * v3
e2 = 0 * v1 + 1/y* v2 + 0 * v3
e3 = 0 * v1 + 0 * v2 + 1/z* v3.
We list the coordinates (remember what are those??) for e1,e2 and e3 as column vectors in a 3x3 matrix
and get a 'change of basis' matrix which has the effect of translating any vector from R3 into our special
vector space. The matrix looks like this :
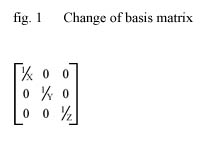
As long as we stick to defining new spaces for which the change of basis matrix looks like above (only
has entries on the diagonal) then we can simplify the multiplication of a vector to the matrix. To do that
we'll need to be able to multiply vectors.
Of course you cannot multiply or divide two vectors but we CAN define what we mean if we write so anyway ;)
We'll define v1 * v2 to mean component-wise multiplication so :
v1*v2 = (v1.x*v2.x, v1.y*v2.y, v1.z*v2.z) - division is defined in a similar way.
If we do that, and create spaces like described above, then we can avoid having to use a 3x3 matrix for space
translations and just say, that to translate a vector from R3 into our space we just multiply it with a vector
describing the basis of our new space. For example we translate x = (3,4,3) into our example space like this :
x2 = x * (1/x, 1/y, 1/z) - or to simplify even further : x2 = x / (x,y,z).
This ONLY holds for change of basis matrices which only has entries on the diagonal (sorry, I know I said
that before) and those spaces just happens to be those you get from R3 when you multiply each basis vector
(e1,e2,e3) with a constant. If you check back, that's exactly what we do to achieve the 'scaling trick' above.
Collision detection :
OK, enough talk - lets get started!
So, we have our guy we wish to move around the world. He's represented by an ellipsoid with a
center (which we will consider his position) and a radius vector defining the ellipsoids size
along the three axis. Like this :
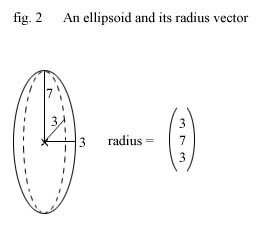
We move our guy though the world by applying a force to him in some direction. This is
represented by a velocity vector. We wish to move the ellipsoid through the world so its
new position equals its current position plus the velocity vector.
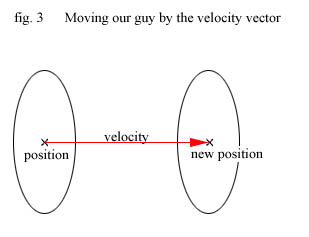
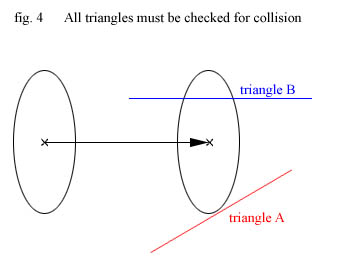
We don't know if we can do that though as there might be something in his way - one or more of
the triangles making up our world might be obstructing his way. We have no chance of knowing
which triangle he might hit, so we'll have to check them all (another motivation to split geometry
up in smaller bits). Also we cannot stop once we find ONE triangle he'll hit - we'll have to check
ALL potential colliders and prepare to collide with the closest one.
Below I have tried to illustrate this by showing what happens if we detect a collision with triangle A
and then stops without checking the rest, including triangle B :
First of all we'll reduce the complexity of the problem greatly by translating everything into
something we'll call ellipsoid space, which is a vector space where the ellipsoid is really
a unit sphere (See section on vector spaces). If we believe we can do that, then for the rest
of this tutorial we can assume our guy is a unit sphere. I believe that..
OK, so we have to check every face. The check for each face can be split into 5 smaller steps
which will give us the following pseudo-code for collision detection :
For every triangle do:
Calculate the plane the triangle lies on.
Calculate the intersection point on the unit sphere where it will hit the plane.
Calculate the point on the plane where the unit sphere collide.
Check if this plane intersection point is in the triangle. If not
calculate the polygon intersection point (if any).
If we hit the polygon and the distance to the intersection is less
or equal to the length of the distance we wish to move we check if
this is the closest hit so far. If it is we write down info about
this collision.
When this algorithm terminates we'll have written down the closest collision (if any) and we
can then handle this information as we'll discuss in the section on collision response.
When the entire process of collision detection and response ends we'll translate the
final result back into standard R3 space to get our final, updated player position.
Below each step is explained in greater detail but make sure you understand the ideas in the
pseudo-code above before you read on. From now on I'll present theory and then implement
that in real C++ code. When finished reading you should study the code for collision detection
in its whole form in the file 'collision.cpp' (using vectormath.cpp and vectormath.h) found in the
downloadable package.
Note that the function in collision.cpp is called from the code taking care of collision
response (in response.cpp)
1) Calculate the plane of a triangle :
This is the easy step! You should all be familiar with planes but let me summarize real
quick what they are in case you forgot. A plane is infinite! That's probably the most important
fact you should remember about planes when we're discussing collision detection. Collision
with a triangles PLANE is NOT necessarily a bad thing and it will most likely happen all
the time. A triangle is a closed subset of the plane it lies on. For example a triangle in
our world in which all its points has a z-value of 0 lies on a plane - namely the infinite
xy-plane which consists of all points in the set A = { (x,y,z) | z=0 } (which is read "
all points (x,y,z) for which z is 0. )
For our use we'll define a plane as a point of origin and a normal vector perpendicular to
all vectors which lies on the plane.
Given a point on the plane and any two (non parallel) vectors lying on the plane we can
calculate the plane normal by using the wedge product (also known as the cross product).
What we want is the plane on which our triangle lies so we just pick any of the triangles
points as the origin of the plane (they all lies on it). Let say our triangle are defined
in a clockwise order like this :
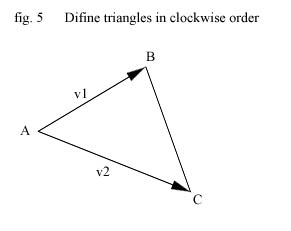
then we chose point A as origin and get two non-parallel vectors on the plane by making
each segment outgoing from A a vector like this :
v1 = B - A;
v2 = C - A;
The plane normal is then given by the wedge product of those two vectors :
inline D3DVECTOR wedge(D3DVECTOR v1, D3DVECTOR v2) {
D3DVECTOR result;
result.x = (v1.y * v2.z) - (v2.y * v1.z);
result.y = (v1.z * v2.x) - (v2.z * v1.x);
result.z = (v1.x * v2.y) - (v2.x * v1.y);
return (result);
}
D3DVECTOR pOrigin = A;
D3DVECTOR pNormal = wedge(v1,v2);
NOTE : The order of the parameters for this function with is important! It defines the direction of
the normal which basically decides if we're looking at a back face or not! Actually it holds as
a general rule that wedge(v1,v2) = -wedge(v2,v1).
Calling it like above is the correct way if your triangles are defined in clockwise order.
We need the normal normalized (its length should be 1) so we also call this function on it :
inline void normalizeVector(D3DVECTOR& v) {
double len = sqrt(v.x*v.x + v.y*v.y + v.z*v.z);
v.x /= len;
v.y /= len;
v.z /= len;
}
normalizeVector(pNormal);
That's it, we now have the plane on which the triangle lies.
Remember that because we work in this special ellipsoid space we need to scale our
triangle into that same space as described in the section on vector spaces (by dividing all its points
with the ellipsoid radius vector)
2) Calculate the theoretical unit sphere intersection point:
In this step we try to predict which point on the unit sphere which will eventually hit
the triangle we're checking against now. And we'll calculate that based on only the position
of the sphere and the plane the triangle lies on. Actually that's not really possible so
what we will calculate is the point on the sphere which will hit the PLANE the triangle
lies on.
That is not easy to do with an general ellipsoid but here we find the first benefit of using
our special ellipsoid space because in that space the problem reduces to figure out which point on a
unit sphere that will hit the plane! This is very easy to do and as you can see from the
picture below it boils down to adding the reversed plane normal to the center of the sphere.
As the normals length is 1 (it's normalized) and the sphere is a unit sphere (its radius is 1)
the length is even correct.
If for some reason you can't work with collision in ellipsoid space you can email me and ask
about how to calculate the intersection point for an ellipsoid but that's a lot of hairy code so I'll
not include it here.
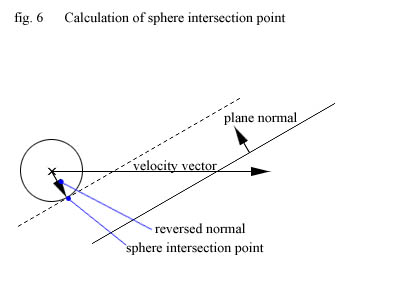
There is a reason why the drawing might seem a little complex! What I have tried to illustrate is that
we calculate the sphere intersection point before we move the sphere! So it is the
point where the sphere will hit the plane if it is moved along its velocity. The dotted line
represent how the plane would be if we moved the sphere close to it.
So the code for this step is simple :
eIPoint = source - pNormal;
3) Calculating plane intersection point :
OK, next step is to figure out where on the plane the sphere will make contact when moved along
the velocity vector. This is simply done by casting a "ray" from the point on the unit sphere
calculated above (the sphere intersection point) in the direction of the velocity vector.
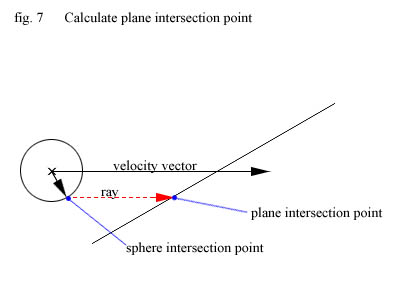
For that we'll need a few new functions :
inline float dot(D3DVECTOR& v1, D3DVECTOR& v2) {
return ( v1.x * v2.x + v1.y * v2.y + v1.z * v2.z );
}
double intersectRayPlane(D3DVECTOR rOrigin, D3DVECTOR rVector, D3DVECTOR pOrigin, D3DVECTOR pNormal) {
double d = - (dot(pNormal,pOrigin));
double numer = dot(pNormal,rOrigin) + d;
double denom = dot(pNormal,rVector);
if (denom == 0) // normal is orthogonal to vector, cant intersect
return (-1.0f);
return -(numer / denom);
}
The parameters should be obvious. One thing to note though is that rVector, the direction of the ray,
must be normalized!
What this function returns is the the distance from the ray origin to the plane along the ray so to
get the plane intersection point we do :
(eIPoint = ellipsoid intersection point from step 2, pIPoint = plane intersection point)
// shoot ray along the velocity vector
distToPlaneIntersection = intersectRayPlane(eIPoint, normalizedVelocity, pOrigin, pNormal);
// calculate plane intersection point
pIPoint.x = eIPoint.x + distToPlaneIntersection * normalizedVelocity.x;
pIPoint.y = eIPoint.y + distToPlaneIntersection * normalizedVelocity.y;
pIPoint.z = eIPoint.z + distToPlaneIntersection * normalizedVelocity.z;
But there is a catch! The code above assumes that the plane is in front of the sphere. That might not
be the case. The plane can span the sphere like shown below. If that happens this step
isn't really very useful. Still we need some point to use as plane intersection point and we
choose to use the point we get by casting a ray from the sphere intersection point along the plane normal.
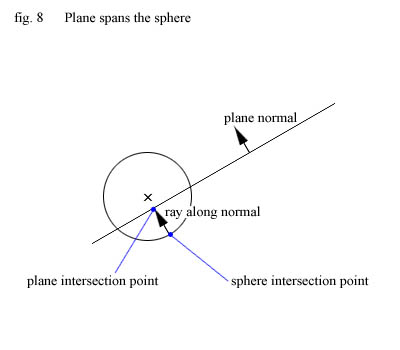
We only want to do this if the plane spans the sphere and how do we check this ?
We need a few more functions :
#define PLANE_BACKSIDE 0x000001
#define PLANE_FRONT 0x000010
#define ON_PLANE 0x000100
DWORD classifyPoint(D3DVECTOR point, D3DVECTOR pO, D3DVECTOR pN) {
D3DVECTOR dir = pO - point;
double d = dot(dir, pN);
if (d<-0.001f)
return PLANE_FRONT;
else
if (d>0.001f)
return PLANE_BACKSIDE;
return ON_PLANE;
}
The function above checks whether a point is in front of, in back of, or on a plane. If the sphere
intersection point is on the backside of the plane then the plane spans the sphere. (Because we'll
only looks at faces where our source point is in front)
So our code to handle spanning planes becomes :
DWORD pClass = classifyPoint(eIPoint, pOrigin, pNormal);
// find the plane intersection point
if (pClass == PLANE_BACKSIDE) { // plane spans sphere
// find plane intersection point by shooting a ray from the
// sphere intersection point along the planes normal.
distToPlaneIntersection = intersectRayPlane(eIPoint, pNormal, pOrigin, pNormal);
// calculate plane intersection point
pIPoint.x = eIPoint.x + distToPlaneIntersection * pNormal.x;
pIPoint.y = eIPoint.y + distToPlaneIntersection * pNormal.y;
pIPoint.z = eIPoint.z + distToPlaneIntersection * pNormal.z;
}
Now we have calculated a plane intersection point no matter if the sphere spans the
plane or not. Let us move on to the next step...
4) Calculate polygon intersection point (if any) :
OK, almost there! Now it's time to calculate the point we're really interested in -
the point where the current triangle will be hit. There are two cases : either we're
in luck and the plane intersection point we calculated above is contained in the
triangle. Or it's not and we'll have to do a little more work.
If the plane intersection point is in the triangle then that point is actually where the
triangle will be hit and we got our polygon intersection point. If not we have the situation
below and both plane intersection point AND sphere intersection point is wrong and will
have to be recalculated.
In this case the polygon intersection point is the point on the edge of the triangle closest
to the plane intersection point and to get the correct sphere intersection point we have to
cast a ray from that point along the reversed velocity vector and see if that ray hits the sphere!
The above three lines might be hard to understand but read them until you do! The drawing might
help you some.
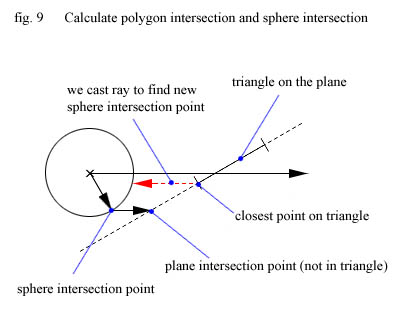
So, it boils down to figuring out if the point is in the triangle or not. What do we know that
can help us do that. Well, at least we know the point lies on the same plane as the triangle, so
we can reduce the problem to a 2d problem. Imagine you draw a triangle on a piece of paper, closes
your eyes and draws a point randomly on the paper. How can you tell if the point is within the
triangle ? Well, you could look but that's cheating ;)
No, lets say you are allowed to draw 3 lines from the point to the 3 points in the triangle. You
are also told the angle between any 2 of those lines. Then you would know the answer because if the
point lies within the triangle then the sum of those angles would be 360 degrees - or 2*PI.
If the point is outside the triangle then the sum will be less. Check the drawing below :
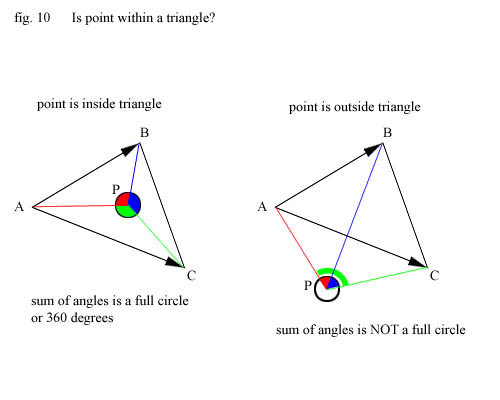
Here is the code to calculate this. (remember that the dot product of two unit vector equals the
cosine to the angle between them)
BOOL CheckPointInTriangle(D3DVECTOR point ,D3DVECTOR a, D3DVECTOR b, D3DVECTOR c) {
double total_angles = 0.0f;
// make the 3 vectors
D3DVECTOR v1 = point-a;
D3DVECTOR v2 = point-b;
D3DVECTOR v3 = point-c;
normalizeVector(v1);
normalizeVector(v2);
normalizeVector(v3);
total_angles += acos(dot(v1,v2));
total_angles += acos(dot(v2,v3));
total_angles += acos(dot(v3,v1));
// allow a small margin because of the limited precision of
// floating point math.
if (fabs(total_angles-2*PI) <= 0.005)
return (TRUE);
return(FALSE);
}
But as mentioned above this function only solves ONE of two possible cases. If the plane intersection
point is NOT contained in the triangle then we have to calculate the closest point on the edge of
triangle. This is done by taking the smallest value of three 'shortest distance to line' calls which
you should all know from standard school math. So :
D3DVECTOR closestPointOnLine(D3DVECTOR& a, D3DVECTOR& b, D3DVECTOR& p) {
// a-b is the line, p the point in question
D3DVECTOR c = p-a;
D3DVECTOR V = b-a;
double d = lengthOfVector(V);
normalizeVector(V);
double t = dot(V,c);
// Check to see if ‘t’ is beyond the extents of the line segment
if (t < 0.0f) return (a);
if (t > d) return (b);
// Return the point between ‘a’ and ‘b’
//set length of V to t. V is normalized so this is easy
V.x = V.x * t;
V.y = V.y * t;
V.z = V.z * t;
return (a+V);
}
D3DVECTOR closestPointOnTriangle(D3DVECTOR a, D3DVECTOR b, D3DVECTOR c, D3DVECTOR p) {
D3DVECTOR Rab = closestPointOnLine(a, b, p);
D3DVECTOR Rbc = closestPointOnLine(b, c, p);
D3DVECTOR Rca = closestPointOnLine(c, a, p);
double dAB = lengthOfVector(p-Rab);
double dBC = lengthOfVector(p-Rbc);
double dCA = lengthOfVector(p-Rca);
double min = dAB;
D3DVECTOR result = Rab;
if (dBC < min) {
min = dBC;
result = Rbc;
}
if (dCA < min)
result = Rca;
return (result);
}
Now all we need is the function which checks if a ray intersects with a sphere :
double intersectRaySphere(D3DVECTOR rO, D3DVECTOR rV, D3DVECTOR sO, double sR) {
D3DVECTOR Q = sO-rO;
double c = lengthOfVector(Q);
double v = dot(Q,rV);
double d = sR*sR - (c*c - v*v);
// If there was no intersection, return -1
if (d < 0.0) return (-1.0f);
// Return the distance to the [first] intersecting point
return (v - sqrt(d));
}
The whole process of finding the final sphere intersection point and polygon
intersection finally boils down to a few lines of code :
// find polygon intersection point. By default we assume its equal to the
// plane intersection point. In that case we already know the distance to it.
polyIPoint = pIPoint;
distToSphereIntersection = distToPlaneIntersection;
if (!CheckPointInTriangle(pIPoint,p1,p2,p3)) { // if not in triangle
polyIPoint = closestPointOnTriangle(p1, p2, p3, pIPoint);
distToSphereIntersection = intersectRaySphere(polyIPoint, -normalizedVelocity, source, 1.0f);
// we cannot know if the ray will actually hit the sphere so we need this check
if (distToSphereIntersection > 0) {
// calculate true ellipsoid intersection point
eIPoint.x = polyIPoint.x + distToSphereIntersection * -normalizedVelocity.x;
eIPoint.y = polyIPoint.y + distToSphereIntersection * -normalizedVelocity.y;
eIPoint.z = polyIPoint.z + distToSphereIntersection * -normalizedVelocity.z;
}
}
5) OK, yes or no - is this triangle hit or not?
This final section is easy. Through the 4 steps above we have obtained three important things :
The distance along the velocity vector we must move to hit the triangle. -1 if no hit.
The point on the triangle which will be hit
The point on the sphere which will hit the triangle.
First of all the distance to the hit must be within reach of our current velocity vector. In
other words we only hit the triangle if distToSphereIntersection is smaller than the length
of the velocity vector.
But even if we do hit the triangle we might have hit another triangle which is closer so we
only save information about this hit if the distance is the smallest one yet. The code looks
somewhat like this (depends on your data structures)
// any chance of hit ?
if ((distToSphereIntersection > 0) && (distToSphereIntersection <= lengthOfVector(velocity)) {
// if first hit, or closest hit so far
if ((foundCollision == FALSE) || (distToSphereIntersection < nearestDistance)) {
nearestDistance = distToSphereIntersection;
nearestSphereIntersectionPoint = eIPoint;
nearestPolygonIntersectionPoint = polyIPoint;
foundCollision = TRUE;
}
}
That was ONE triangle, now all that remains is to repeat ;)
Collision Response :
So now you know how to check if your sphere collides with any of the triangles in your world given a
certain velocity vector. But what do we do when a collision actually occurs? The easiest way to handle
a collision is to simply stop and not allow the move when a collision is detected. On the other hand -
that is not how the professionals do is it? No, we want fancy collision response like sliding along the walls,
automatically climbing stairs and automatically bumping over smaller obstacles on the ground.
Actually we turn out to be in luck since all these things come automatically from our implementation of
sliding!
So what exactly do we mean by sliding? Well, what we want to do if we collide with a triangle in our world is
to move close to it, change the direction of our velocity vector and then continue movement in a new direction.
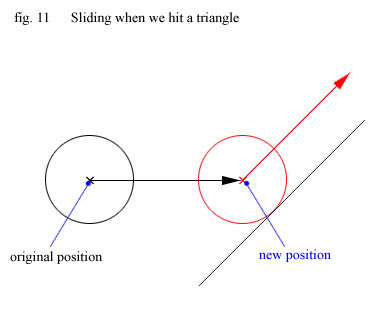
I'll now introduce the idea of the sliding plane. The sliding plane is, as the name implies, the plane
along which we will continue our movement. From the picture above you might get the idea that the sliding plane is identical
with the plane on which the colliding triangle lies. In some cases this is also correct but as the picture below
demonstrates it is not always the case :
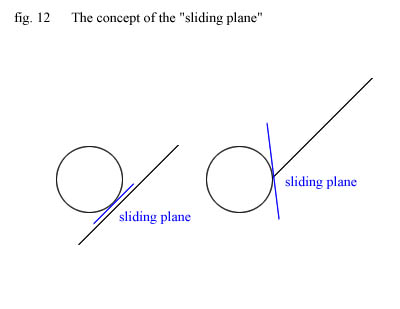
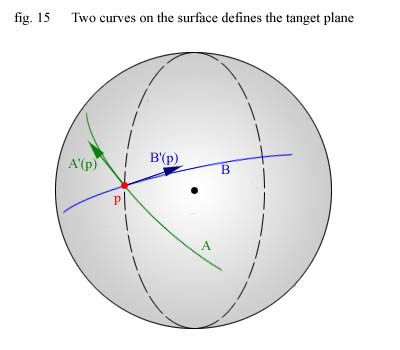
Lets generalize the idea of the sliding plane. What does the two planes above have in common ? They are both the
tangent plane to the sphere in the sphere intersection point from the section on collision detection.
So we have to find a way to calculate the tangent plane for the sphere, given a point on its surface. Remember how
we represent planes in this tutorial ? We define them by a point and a normal to the plane, right ?
We already have the point - namely the sphere intersection point - so our task at hand is really to calculate the
normal to the tangent plane of the sphere in the sphere intersection point, right ?
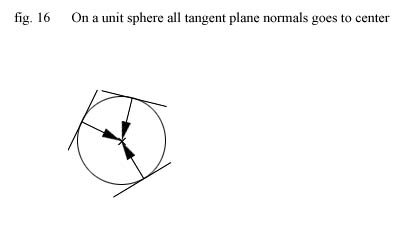
It turns out that once again our choice of working in a special ellipsoid space saves us from
a lot of computations
because the normal to the tangent plane at any point on a unit sphere is just the vector going from the point on the surface
to the center of the sphere! This is not the case with the more general ellipsoid shape !!
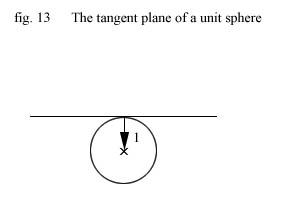
So calculating the sliding plane is easy in ellipsoid space and boils down two lines of code :
D3DVECTOR slidePlaneOrigin = nearestPolygonIntersectionPoint;
D3DVECTOR slidePlaneNormal = newSourcePoint - nearestPolygonIntersectionPoint;
Well, this isn't really a satisfying explanation is it ? What if we hadn't worked in this fancy ellipsoid space ?
Couldn't we have computed this sliding plane anyway ?
If you couldn't care less you can skip the next section and continue reading at the section called :
'Collision Response - continued'.
The rest of you, get ready for some math because of course we can calculate the sliding plane for any spherical or
ellipsoid shape. The next section will also make it clear why the calculations are so simple for the unit sphere.
The tangent plane of any spherical or ellipsoid shape:
Anyone still with me ? Cool, lets get enlightened then :) Again this will have to be a little quick and I
cannot cover every detail because then this would become a math tutorial. What I try to do is introduce
exactly enough concepts for you to understand the important part of this section - the calculation of the
general tangent plane.
The answer lies in the theory of differential geometry of regular surfaces. I will not go into the definition
of regular surfaces but think of them as certain 'smooth' surfaces in 3D - like the surface of an ellipsoid or
sphere.
Ok, first lets think about how a tangent plane is defined. Most of you will have an intuitive understanding of
what it is but not all have been introduced to a precise definition before.
Lets go one dimension down and look at what we know about tangents in 2D. From school we know that the tangent
to a curve looks like on the picture below and is calculated by differencing its function:
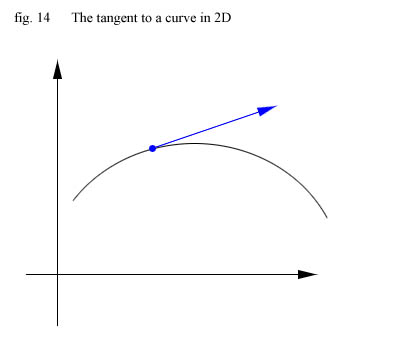
On the drawing above the curve is in 2D but we could actually consider it as lying on a plane in 3D right ? Namely
the xy plane in standard 3D. What if I told you that we could have the curve lying on a regular surface like a sphere or
ellipsoid! It would run over the surface and be parameterized by one single variable t.
This is just like in 2D where the curves we know are parameterized by a single variable x (we consider a
curve in 2D as a functionf(x) = y, right ? ). To do that we will have to change the definition of the
function for the curve but it would still be a function of one variable and we would know how to differentiate it.
In 3D a curve is defined by 3 functions, each one describing the value of one of the 3 coordinates given a parameter
t. So if we call the curve A then its function becomes :
the velocity vector gets very small
Ok, what about this projecting thing ? Well, it just so happens that it does exactly what we want. It generates a
vector on the sliding plane we can move along and the more directly we hit the triangle the less do we slide.
Check the drawing :
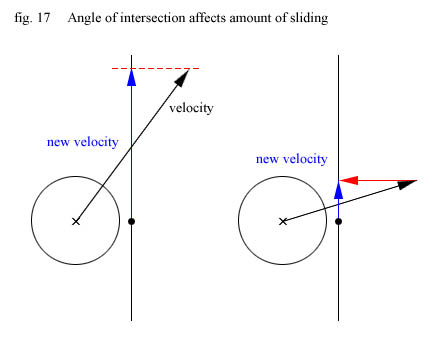
To accomplish all this we need to be able to project the velocity vector to a plane, but as it turns out we already
have all the functions we need. We'll use the intersectRayPlane from the collision detection section and calculate
the projection as the intersection we get by casting a ray from the destination point, along the sliding plane normal,
to the sliding plane. So the code becomes :
// Determine the sliding plane (we do this now, because we're about to
// change sourcePoint)
D3DVECTOR slidePlaneOrigin = nearestPolygonIntersectionPoint;
D3DVECTOR slidePlaneNormal = newSourcePoint - nearestPolygonIntersectionPoint;;
// We now project the destination point onto the sliding plane
double l = intersectRayPlane(destinationPoint, slidePlaneNormal,
slidePlaneOrigin, slidePlaneNormal);
D3DVECTOR newDestinationPoint;
newDestinationPoint.x = destinationPoint.x + l * slidePlaneNormal.x;
newDestinationPoint.y = destinationPoint.y + l * slidePlaneNormal.y;
newDestinationPoint.z = destinationPoint.z + l * slidePlaneNormal.z;
// Generate the slide vector, which will become our new velocity vector
// for the next iteration
D3DVECTOR newVelocityVector = newDestinationPoint - collision->nearestPolygonIntersectionPoint;
// Recurse. Pos is where we expect our final position
finalPos = collideWithWorld(newSourcePoint, newVelocityVector);
// return the final result
return finalPos;
Gravity :
What if we want gravity in our world ? Will that be hard ?
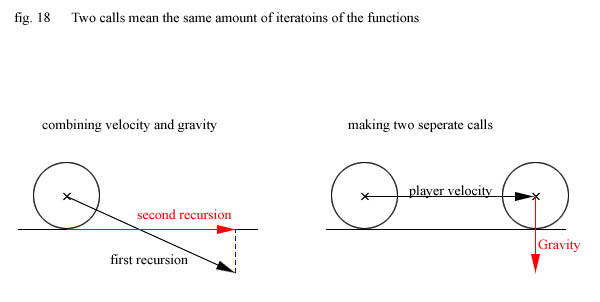
No not at all, each frame you just make two calls to the collision detection routines - one time with the player
velocity and another time with a gravity vector. You can combine the two vectors and then just call the routines
once with a vector v = velocity + gravity but that will make climbing stairs become more difficult as the velocity
vector must be much longer for the projected vector to slide upwards enough when you hit the edge of a stair (think
about it).
In most cases making two separate calls wont even affect the total numbers of calls to the functions because when
moving along flat ground if you combine velocity and gravity you will have two recursions as shown on the drawing
below. If you first move along the ground with the velocity you will not hit anything, and the second call with
the gravity vector will collide and not recurse because the hit is perpendicular to the surface.
Error handling :
You're working with floats and floats only have a limited precision! Thus you are bound to get errors now and then.
By errors I mean moving into solid geometry because the routines return the wrong results or falling though the ground.
Still, in my humble opinions collision detection is one of the places where you should be extra careful not
to have errors! It should never happen that the player falls through the ground and end up outside your world. And it should
never happen that the player is stuck because you allowed him to move inside a solid block of stone!
Now, these statements might seem self contradictable - first I say errors are bound to occur and the next second I say
they should never happen. Well, the solution is to be ready for the errors and handle them so the player never notice
they are there! There is no shame in errors due to the limited precision of floats - every engine has them, even the
Quake engine! In the original Quake John Carmack introduced several ugly hacks to get a player "unstuck" if the engine
found out he was.
There is no single solution so what I'm going to do here is present you my idea of how to avoid getting stuck. The idea
is based on the fact that even if we might not be able to check before a move if we are going to get stuck we will
know it in the next iteration of the collision routines. When we have calculated the polygon intersection point as described
in the section on collision detection we check if that point is inside the sphere. Of course it never should be but
my experiences tells me it happens now and then.
It's easy to check if a point is inside a sphere :
BOOL CheckPointInSphere(D3DVECTOR point, D3DVECTOR sO, double sR) {
float d = lengthOfVector(point-sO);
if(d<= sR) return TRUE;
return FALSE;
}
If we find out that our player (sphere) is stuck we set a certain flag in the structure containing the collision data and
then we can handle that in our collision response routine. The way we handle it is to introduce the idea of the
last safe position. Each time we receive data from our collision routines we check if we are stuck.
If not, we update the last safe position and set it to the position we called the routines with this time. If we are
stuck we stop recursing and set the player position back to the last safe position.
Multiple meshes :
What if our world is split up into many small collections of triangles ? Well, first of all, this is actually a very good
idea! The fewer triangles you check in each call the faster the engine will run. What you do is to keep a structure of
collision data which you pass along to each mesh within reach! The structure should contain information about the closest
hit so far etc. etc. and must be reset for each new call to the main collision detection function!
Before checking a mesh you can then first check if it's within reach. You can do this in any way you like - I use a bounding
sphere around the mesh and check if my current velocity will bring me inside that sphere. If it will I check the mesh.
After all meshes has been checked you retrieve the collision data from the structure and react like described in the section
on collision response.
Dynamic geometry :
So far we have only looked at geometry positioned in world space - i.e. the world matrices for all meshes has been the
identity matrix. In a real game you will have a lot of moving geometry. As an example you can check the door or lift in
the demo program that comes with this tutorial. The fact that you cannot walk through the door when it is closed seems obvious
but when you think about it, it really isn't.
Of course I don't change all coordinates in the mesh making up the door when it opens - I just change its world matrix.
But that means that the data the collision routines receive is the same no
matter if the door is open or closed! (think about
it!).
The solution is to move the sphere from world space into object space before you check the triangles in the object. This is
done like this :
D3DMATRIX invWorldMatrix;
// invert the objects world matrix
if (FAILED(D3DMath_MatrixInvert( invWorldMatrix, savedWorld )))
Log("could not invert world matrix");
D3DVECTOR translatedDestination;
D3DVECTOR originalSource, originalVelocity;
// Remember - this scales from ellipsoid space to R3
originalSource = sourcePoint * ellipsoidRadius;
originalVelocity = velocity * ellipsoidRadius;
// translate after animation
D3DMath_VectorMatrixMultiply( translatedSourcePoint, originalSource, invWorldMatrix);
D3DVECTOR originalDestination = originalSource + originalVelocity;
D3DMath_VectorMatrixMultiply( translatedDestination, originalDestination, invWorldMatrix);
translatedVelocity = translatedDestination - translatedSourcePoint;
// convert data back to ellipsoid space
translatedVelocity /= ellipsoidRadius;
translatedSourcePoint /= ellipsoidRadius;
Then check all triangles with the translated source and velocity.
It takes a little more to implement lifts. Not because you don't check the right position of the lift
mesh - but because the lift moves! We have to check if it hits the player and if so the player should be
pushed upwards with the lift! Lifts going down is automatic because of gravity.
To handle lifts you should for each object keep a vector called objectVelocity and if the
player collides with an object where this vector is not the zero-vector then the player should become
sort of a child-object to the lift and the player movement becomes the objectVelocity
plus the player velocity plus gravity!
I will not provide any code for this because such code is quite engine specific and it depends very much
on how you handle your objects animations etc. So consider this last bit a source of inspiration for
implementing the stuff yourself ;)
Last remarks :
Well, that's about all for now.
Hope you found this doc useful - and btw : If you do make anything public using
these techniques please mention me in your greets or where ever you se fit.
I do love to see my name in a greeting :=)
Thanks to Paul Nettle for sharing his ideas about the original algorithm and to Soren Seeberg a.k.a. ZeeGate who went
though all the pain of creating those nifty pictures you saw though the document.
Keep on codin'
Kasper Fauerby a.k.a. Telemachos
November, 2000